1.6 Momentum

Momentum (vector)

Momentum is defined as the product of mass and velocity.

p = mv

‘m’ is the mass and ‘v’ is the velocity

Momentum is a useful quantity to consider when bodies are involved in collisions and explosions. It is defined as the mass of the body multiplied by its velocity and is measured in kilogram metre per second (kg m/s) or newton second (N s).

Impulse (vector)

Impulse is the change in momentum or the product of force and time duration of collision.

Impulse = Change in momentum         

Impulse = mv-mu

Or

Impulse = product of force and time     

Impulse = Ft

Therefore, the equation

Ft = mv – mu

Where F = Force, m = mass, v = final velocity, u = initial velocity

Resultant force can be defined as the change in momentum per unit time;

$$F={{mv – mu}\over{t}}$$

Or

$$F={{Δp}\over{Δt}}$$

Uppercase delta (Δ) means “change” or “the change”

Therefore, Δp = Change in momentum and Δt = change in time

The Principle of the conservation of momentum

The law of conservation of momentum states that the total momentum of a closed system does not change. This means that when two objects collide the total momentum of the objects before the collision is the same as the total momentum of the objects after the collision.

    Momentum before Collision = Momentum after Collision

Example 01:

A wooden cart with mass 15kg moving with velocity of 5m/s to the right collides with a another wooden cart of mass 11kg moving with a velocity of 2m/s to the left.

The wooden cart of mass 11kg has a velocity of 1.6m/s to the right after collision. Find the final velocity of the 1500kg wooden cart.

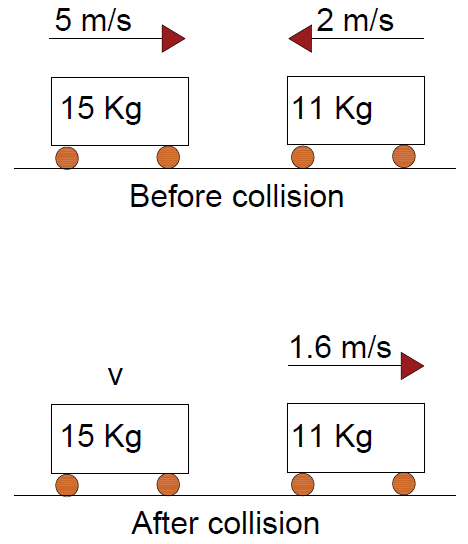
Consider that the positive direction is to the right and v is also to the right

Momentum before

Collision = 15 x 5 – 11 x 2 = 75 kgm/s – 22kgm/s = 53 kgm/s

Momentum after

Collision = 15 x v + 11×1.6 = 53 (Momentum is conserved)

                = 15v + 17.6 = 53

                = 15v = 35.4                           

v = 2.36m/s

Example 02:

A truck of mass 60 kg moving with velocity 3 m/s collides and couples with a stationary truck of mass 30 kg. The two move off together with the same
velocity v. Find v.

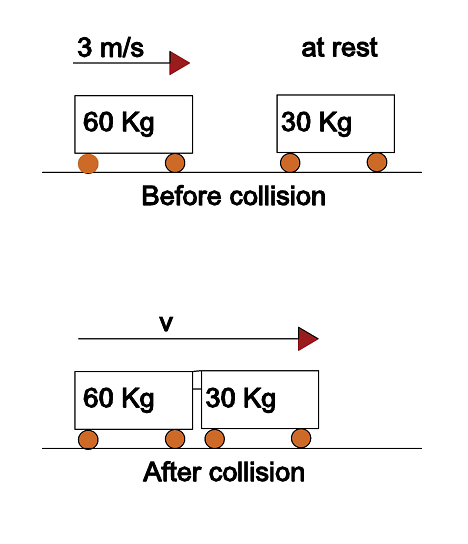
Total momentum before collision is
(60 kg × 3 m/s) + (30 kg × 0 m/s) = 180 kg m/s

Total momentum after collision is
(60 kg + 30 kg) × v = 90 kg × v

Since momentum is not lost
90 kg × v = 180 kg m/s

v = 2 m/s