1.5 Forces
1.5.1 Effects of forces
A force is a push or a pull. It can cause a body at rest to move, or if the body is already moving it can change its speed or direction of motion. A force can also change a body’s shape or size.
Extension Load Graph (Experiment)

Step 01 : Set up all apparatus except the known mass as shown in the diagram above.
Step 02 : Measure and record the initial length of the spring against the meter ruler. At this stage extension is 0 cm.
Step 03 : Add 20g of mass to the end of the spring and record new length of the spring. Calculate and record its extension by subtracting the initial length from the new length.
Step 04 : Add another 20g to the spring and record its length again. Calculate and record its extension by subtracting the initial length from this length.
Step 05 : Repeat steps 3 and 4 until all the masses are hanging from the end of the spring.
Step 06 : To calculate the load on the spring at each stage, use the formula W=mg, where ‘W’ is weight, measured in N, ‘m’ is the total mass the spring is carrying at that stage, measured in kg, and g is the acceleration of free-fall, which is approximately 9.8m/s2.
Step 07 : Plot a graph of extension (cm) against load (N). Draw a line of best fit.
Result Table
| Mass (g) | Mass (Kg) | Load (N) | Spring Length (cm) | Extension (cm) |
|---|---|---|---|---|
| 0 | 0 | 0 | 20 | 0 |
| 20 | 0.02 | 0.2 | 22 | 2 |
| 40 | 0.04 | 0.4 | 24 | 4 |
| 60 | 0.06 | 0.6 | 26 | 6 |
| 80 | 0.08 | 0.8 | 28 | 8 |
| 100 | 0.1 | 1 | 30 | 10 |
| 120 | 0.12 | 1.2 | 34 | 14 |
| 140 | 0.14 | 1.4 | 42 | 22 |

Resultant Force
A resultant force, also called a net force, is a force equal to the sum of all forces applied to an object. (Also note that force is a vector)
Usually more than one force acts on an object. As a simple example, an object resting on a table has a downward force weight and upward force due to the table supporting it. Since the object is at rest, the forces must balance
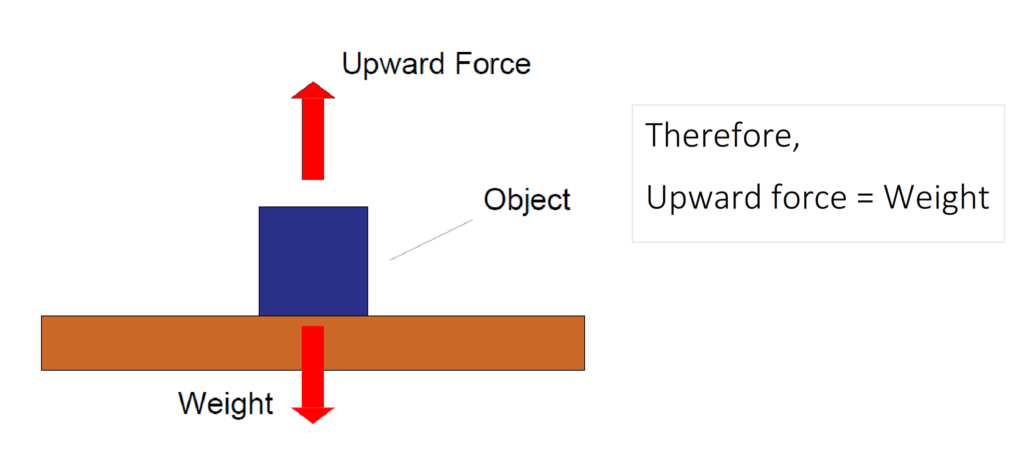
Note: If there is no resultant force on a body it either remains at rest or continues at constant speed in a straight line.
Fig 01 : Resultant force is 15N forward direction
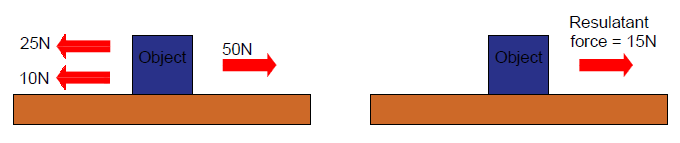
Fig 02 : Resultant force is 0 N object remains at rest

Friction
Friction is a force between two surfaces which impedes motion and results in heating
If a friction force acts on a moving object and there is no forward force, there is a resultant force backwards on the object and it will slow down or cause the object to stop.
Example:

A moving vehicle such as a bicycle, car or plane is subject to air resistance. The air exerts an opposing friction force. The greater this air friction, the greater the vehicle’s fuel consumption is. Or, in the case of cycling, the more effort you must make to stay in motion.
Solid Friction:
Solid friction is the resistive force that occurs when two surfaces are in contact and impedes motion.
It generates heat due to the interaction of the surfaces.
The roughness of the surfaces and the force pressing them together influence the friction.
Friction (Drag) in a Liquid:
When an object moves through a liquid, it experiences drag (a type of friction).
Drag opposes the motion, making it harder for the object to move through the liquid.
This resistance increases with the speed of the object and the viscosity of the liquid.
Friction (Drag) in a Gas (Air Resistance):
Drag also acts on an object moving through a gas, like air resistance.
Air resistance is a form of drag that increases with the object’s speed and surface area.
This force opposes motion and reduces the speed of the object.
Hooke’s law
Hooke’s law states that, for the region up to the limit of proportionality, extension is proportional to load (F ∝ x).
Therefore, the graph is a straight line up to the limit of proportionality. (Check graph 1)
Hooke’s law: F = Kx
‘F’ is the force (N) , ‘k’ is the spring constant (N/m) and ‘x’ is the extension in m/cm/mm
Therefore, spring constant can be defined as force per unit
extension;
$$K={{F}\over{x}}$$
Limit of Proportionality:
The limit of proportionality refers to the point on a load-extension graph where the extension of a material stops being proportional to the load applied.
Up to this point, Hooke’s Law applies (extension ∝ load). Beyond this, the material may no longer return to its original shape.
Equation
F = ma
This equation states that force (F) is the product of mass (m) and acceleration (a).
Both force and acceleration act in the same direction.
This is Newton’s second law of motion, showing how force affects the motion of an object.
Motion in a Circular Path:
For an object moving in a circular path, the force (centripetal force) acts perpendicular to the motion.
(a) If the force increases, the speed of the object increases, assuming mass and radius are constant.
(b) If the force increases, the radius of the path decreases, assuming mass and speed remain constant.
(c) An object with greater mass requires a larger force to maintain the same speed and radius.
The diagram below shows a satellite that is moving at a uniform rate in a circular orbit around the Earth.
The satellite is pulled towards the Earth (at 90 degrees to its direction of travel). This causes it to travel in a circular

Describes the motion of this satellite?
The satellite moves at a constant speed (uniform rate), meaning its speed does not change as it orbits the Earth.
However, the satellite is constantly changing direction because it is moving in a circular path. This change in direction means the satellite is accelerating, even though its speed remains the same. This is known as centripetal acceleration.
The force that keeps the satellite in its circular orbit is the gravitational pull of the Earth. This force always acts perpendicular (at 90 degrees) to the satellite’s direction of travel, towards the center of the Earth.
Since the force is acting towards the center of the orbit, it is called the centripetal force, and it prevents the satellite from flying off in a straight line by constantly pulling it inward, causing it to follow a curved, circular path.
In summary, Satellite is moving with uniform speed but its direction of motion is changing at each point. Hence, velocity changes. If the velocity is changing then it means the motion is accelerated.
1.5.2 Turning effect of forces
Moment or Turning effect is the product of force and perpendicular distance from pivot.
Moment of force = F x d
‘F’ is the force and ‘d’ is the perpendicular distance from pivot (usual unit m).
Examples of turning effect of force:
1. A person removes a bottle’s cap by pushing down the bottle opener’s lever.
2. A force is applied to a door knob and the door swings open about its hinge.
3. A worker applies a force to a spanner to rotate a nut.

Moment of force = F x d
Convert to metres 20cm/100 = 0.2m
Moment of force = 40×0.2m
Moment of force = 8Nm
Increasing force or distance from the pivot increases the moment of a force

Case 01: Moment of Force = 0.2 x 40 = 8Nm
Case 02: Same nut but shorter spanner
Find out the force
8Nm = 0.15 x Force
Force = 8Nm/0.15m = 53..3N
This means that if you increase the distance from pivot you have to use less force. Shorter the distance from pivot you have to use more force.
Principle of moments
The Principle of Moments states that when a body is balanced, the total clockwise moment about a point equals the total anticlockwise moment about the same point.
Example 01:

When an object is balanced (in equilibrium) the sum of the clockwise moments is equal to the sum of the anticlockwise moments.
Convert cm into m and g into Kg
Anticlockwise moment = 0.8m x (0.5Kg x 9.8 m/ s2) = 3.92Nm
Clockwise moment = 0.8m x (0.5Kg x 9.8 m/s2 ) =3.92Nm
Anticlockwise moment = Clockwise moment, so the plank balances
Example 02:
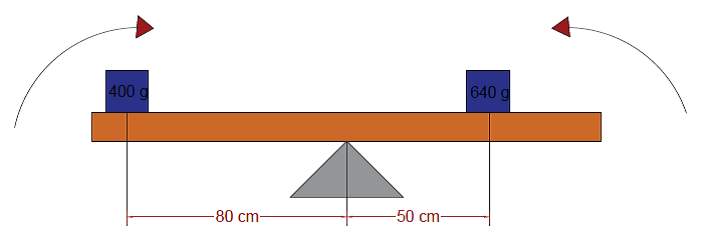
Convert cm into m and g into Kg
Clockwise moment = 0.8m x (0.4Kg x 9.8 m/s2 ) = 3.14Nm
AntiClockwise moment = 0.5m x (0.64Kg x 9.8 m/s2 ) = 3.14Nm
Anticlockwise moment = Clockwise moment, so the plank balances
Apply the principle of moments to other situations, including those with more than one force each side of the pivot
The following diagram below shows the effect of having more than one force on each side of the pivot
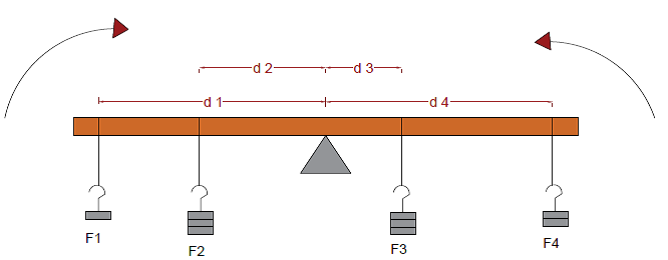
(F1 x d1) + (F2 x d2) = (F3 x d3) + (F4 x d4)

(10N x 90cm) + (30N x 50cm) = (30N x 20cm) + (20N x 90cm)
9Ncm + 15Ncm = 6Ncm + 18Ncm
Anticlockwise moment = Clockwise moment, so the plank balances
24Ncm = 24Ncm
Conditions for equilibrium: When there is no resultant force and no resultant moment, an object is in equilibrium
1.5.3 Centre of gravity
The center of gravity is an imaginary point where the whole weight of the body is concentrated.
What is a plane lamina?
- A body whose mass is concentrated in a single plane
Experiment to determine the position of the centre of mass of a plane lamina
Step 01 : Cut an irregular shape from cardboard
Step 02 : Make three holes close to the edges of the irregularly shaped cardboard as show below

Step 03 : Suspend the object to swing freely on a needle or nail through one of the holes created

Step 04 : Attach a plumb line to the needle or nail and mark its position on the cardboard with the help of a rule


Step 05 : Repeat steps 3 and 4 for the remaining holes, marking the positions of the plumb-lines carefully
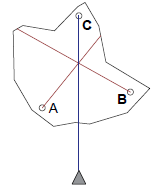
Step 06 : Locate the intersection of the three lines drawn; this indicates the centre of gravity of the object.

More Stable objects usually have lower center of gravity and large base area.
Objects with higher center of gravity and small base area, are easier to topple.
An object would fall over, if it’s center of gravity does not pass through its base when it is tilted.

Thank you
Lowkey helpful shit, easy to understand