1.1 Physical quantities and measurement techniques

The SI (International System of Units) unit of length is the metre(m) (Other usual units of Length: Km, cm, mm etc.)

Powers of ten: This is a neat way of writing numbers, especially if they are too large or too small.

Rulers can be used to measure small distances of a few cm. They are able to measure to the nearest mm.

When measuring larger distances (of a few metres) a tape measure is more appropriate or, when measuring even larger distances, a trundle wheel.

1 killometer (Km)	$$1000m\;or\;10^{3}m$$
1 centimetre (cm)	$$0.01m\;or\;10^{-2}m$$
1 millimetre (mm)	$$0.001m\;or\;10^{-3}m$$
1 micrometre (μm)	$$0.000001\;or\;10^{-6}m$$
1 nanometre (nm)	$$0.000000001\;or\;10^{-9}m$$

Question: Calculate the length of the cotton

Ans: start : 2.4cm, end: 15.6cm
Therefore, 15.6 cm – 2.4cm
Length of the cotton is 13.2cm

Parallax error:

Occurs when the measurement of an object’s length is more or less than the true length because of your eye being positioned at an angle to the measurement markings.

Volume

Volume is the amount of space occupied. The unit of volume is the cubic metre but as this is quite large, for most purposes the cubic centimetre is used.

Volume = length × breadth × height

Find the volume of the cube shown below

$$1cm\;x\;1cm\;x\;1cm\;=\;1cm^{3}$$

$$Convert\;1cm^{3}\;into\;1m^{3}?$$

$${{1}\over{100}}m\;x\;{{1}\over{100}}m\;x\; {{1}\over{100}}m\;= {{1}\over{1,000,000}}\;m^{3}\;$$

Therefore,$$1cm^{3}\;=\;1^{-6}m^{3}$$

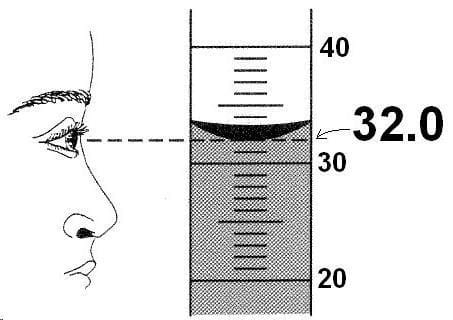
The volume of a liquid may be obtained by pouring it into a measuring cylinder.

When making a reading your eye must be level with the bottom of the curved liquid surface, i.e. the meniscus.

Liquid volumes are also expressed in litres (l);

$$1\;millilitre\;(1\;ml)\;=\;1cm^{3}$$

$$1000\;cm^{3}\;=\;1\;litre$$

Time

The SI unit of time is the second (s)

To measure an interval of time in an event, first choose a timer that is accurate enough for the task. A stopwatch is adequate for finding the period in seconds

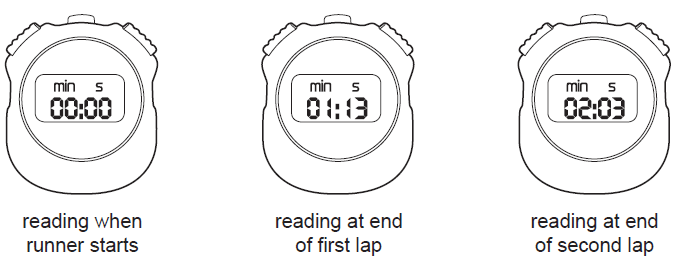
Time Taken for the first lap = 01 min and 13 Seconds

Total Time Taken = 02 min and 03 Seconds

What is the time taken for the runner to run the second lap?

Answer should be 0 min 50 Seconds

Period of a simple pendulum

Attach a small metal ball (called a bob) to a piece of string, and suspend it as shown below.

Pull the bob a small distance to one side, and then release it so that it oscillates to and fro through a small angle.

One oscillation is from A to O to B to O to A. The time for one oscillation is the period T.

Scalars and Vectors (Supplement)

Vectors : have a magnitude and a direction

Scalars : have a magnitude only.

Vectors	Scalars
Displacement	Length , Area, Volume
Velocity	Mass
Acceleration	Speed
Momentum	Pressure
Force	Density
Weight	Temperature
Electric field strength	Time
gravitational field strength	Energy

Resultant of two vectors at right angles

1. By calculation

2. Graphical Method

/20

1.1 Physical quantities and measurement techniques Quiz

Physics quiz helps us to increase our knowledge

1 / 20

The diagram shows a pendulum. The pendulum bob swings repeatedly between points M and N.

A student starts a stop-watch when the bob reaches point M.
He counts each time the bob changes direction and stops the watch on the tenth change in
direction.
The watch shows a time of 12.0 seconds.
What is the period of the pendulum?

0.60 s

1.2 s

2.4 s

12.0 s

2 / 20

A student uses a metre rule to measure the length of a sheet of paper.
Which measurement is shown to the nearest millimetre?

0.3 m

0.29 m

0.293 m

0.2932 m

3 / 20

The diagram shows a rectangular metal sheet close to two rulers.

What is the area of the metal sheet?

$700cm^2$

$875cm^2$

$900cm^2$

$1125cm^2$

4 / 20

Which piece of apparatus is the most suitable for measuring the length of a pencil

vernier calipers

micrometer screw gauges

measuring tape

ruler

5 / 20

A student has a measuring cylinder containing water and also has a balance.
Which of these could she use to find the volume of a small metal sphere?
She has no other apparatus.

either the measuring cylinder containing water or the balance

the measuring cylinder containing water only

the balance only

neither the measuring cylinder nor the balance

6 / 20

Which of the following quantities has only magnitude but no direction?

Acceleration

Force

Time

Momentum

7 / 20

The diagram shows a stone of irregular shape.

Which property of the stone can be found by lowering it into a measuring cylinder half-filled with
water?

length

mass

volume

weight

8 / 20

Which list places units of length in increasing order of magnitude (size)?

cm , mm , m

mm , cm , m

mm , m , cm

m , mm , cm

9 / 20

A lump of modelling clay is moved from a small measuring cylinder to a large measuring cylinder
that has twice the diameter.

By how much does the reading on the large cylinder go up?

$10cm^3$

$20cm^3$

$40cm^3$

$80cm^3$

10 / 20

A measuring cylinder is used to measure the volume of a quantity of water.
Which measuring technique would “not” improve the accuracy of the measurement?

making sure that the measuring cylinder is vertical

making sure that the water surface is at eye level

reading the top of the water meniscus

using the smallest measuring cylinder available that will contain all the water

11 / 20

When measuring the volume of a liquid in a measuring cylinder, where should you read the measurement to ensure accuracy?

At the top of the meniscus

At the bottom of the meniscus

At the middle of the meniscus

At any point along the meniscus

12 / 20

A student measures the volume of a quantity of water.
Which apparatus is suitable?

a balance

a measuring cylinder

a ruler

a thermometer

13 / 20

A student investigates a pendulum.
He measures the time for the pendulum to complete 20 oscillations.
He repeats the experiment three more times.
The readings are shown.

What is the average period of the pendulum?

0.88 s

0.92 s

17.6 s

18.4 s

14 / 20

A pendulum makes 50 complete swings in 2 min 40 s.
What is the time period for 1 complete swing?

1.6 s

3.2 s

4.8 s

6.4 s

15 / 20

When measuring the length of an object using a ruler, how can parallax error be minimized?

Measure at an angle to the ruler

Measure from above, with your eyes directly in line with the measurement mark

Use a longer ruler

Hold the object at a distance from the ruler

16 / 20

Diagram 1 shows a solid, rectangular-sided block.

Diagram 2 shows the same block from the front and from the side.
Metre rules have been shown close to the edges of the block.
What is the volume of the block?

$120cm^3$

$168cm^3$

$264cm^3$

$1155cm^3$

17 / 20